Flexible shift scheduling with Excel/JuMP: UBC LIFE Collegium
See my GitHub for the Excel sheet and full Julia code.
This scheduling problem is much more exciting than my first project because of the nature of flexible shifts. In a predetermined shift problem, the shifts are decided first and then employees provide their availability for those shifts. However, in a flexible shift problem, employees give their availability for all relevant working hours first. Then, the shifts are created based on employee availability (and on various constraints).
In creating a flexible assignment model, the optimization variable, objective function, and constraints become much more interesting. Since employees now give their availability for time and day instead of simple set shifts, the data can naturally be represented with an extra dimension. The objective function must now reward continuous shifts to avoid scattered, “swiss-cheese” schedules. Finally, there are new constraint considerations such as minimum shift length.
A Very Quick Overview
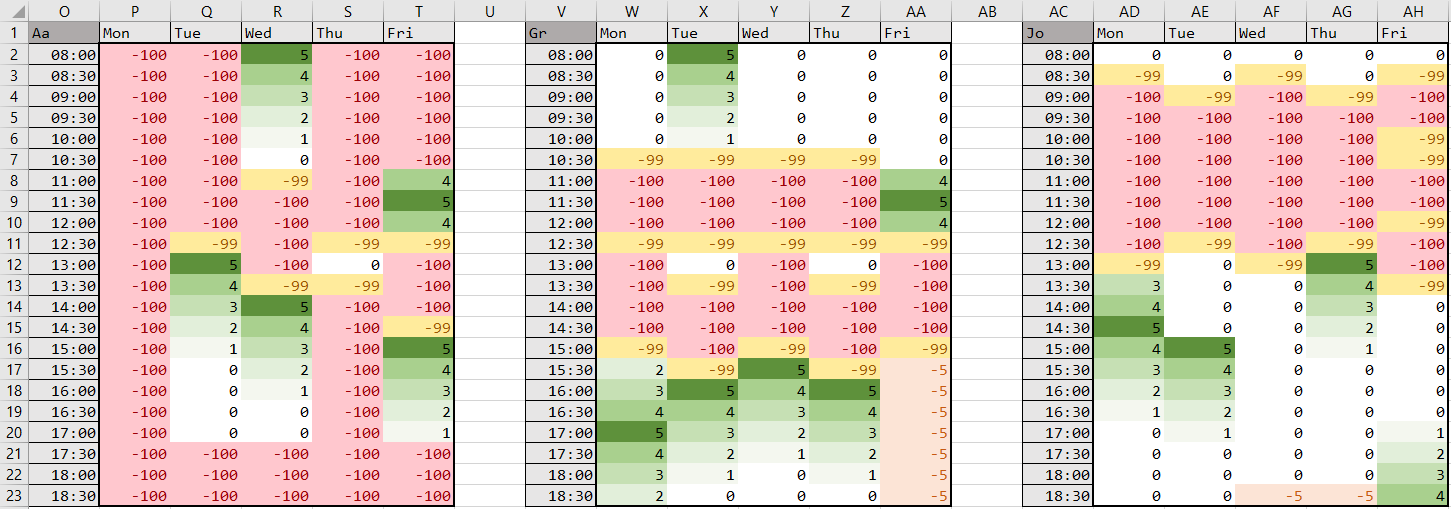
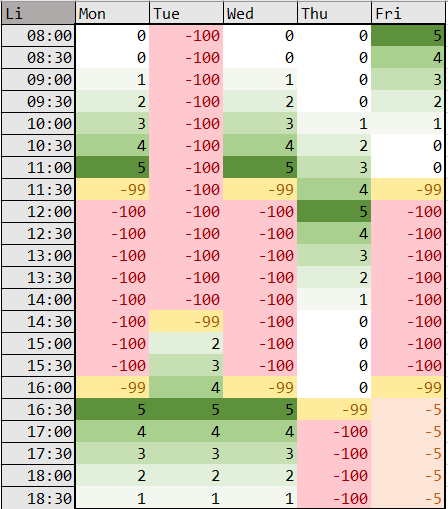
Employees provide their availability and preferences for the week within a timetable. Every employee’s availability timetable is collected on a common Excel sheet like so:
The values in the tables denote the following:
Now, the assignment problem is solved with Gurobi and JuMP. The finished schedule is produced and read into another sheet within the same workbook.
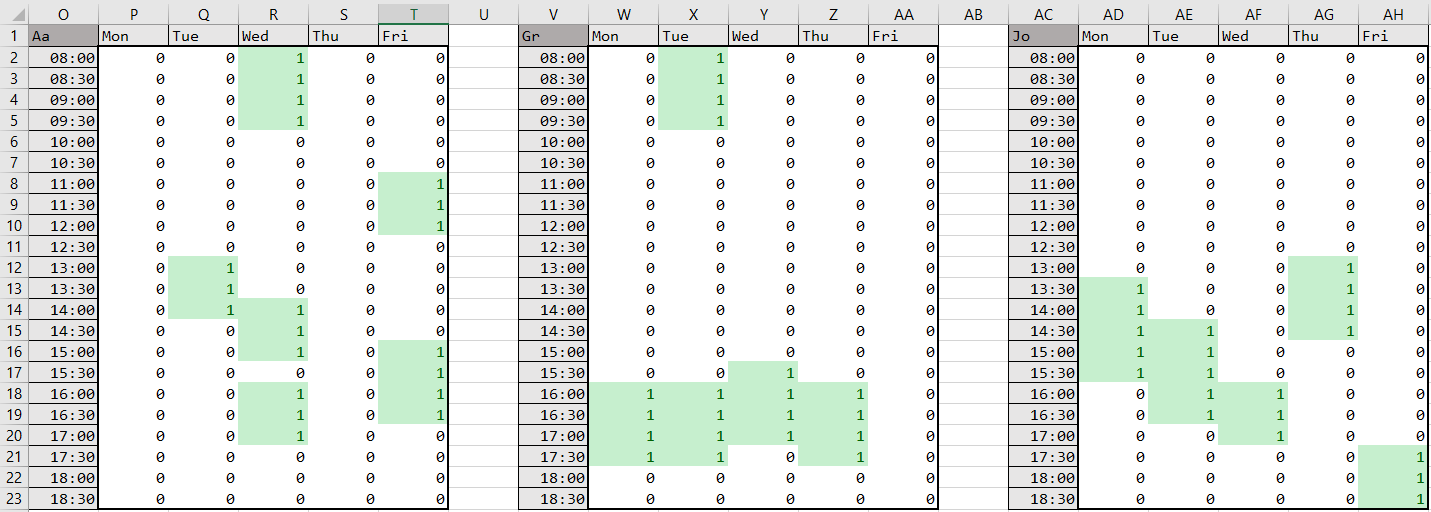
Here, the shifts are shown as follows:
The schedule takes into account:
- Minimum shift length
- Maximum number of opening/closing shifts
- Maximum/minimum weekly working hours
- Maximum/minimum number of employees working a given timeslot
- A collective meeting time in which all employees are scheduled.
Problem Specifications
The problem is described with respect to the needs of UBC LIFE Collegium 2018-19, but serves as a basic framework for flexible shift scheduling.
The LIFE Collegium is open from Monday to Friday, 08:00 to 19:00. We break each day into 22 half-hour slots. For each day, the first shift (08:00) is the opening shift and the last or 22nd shift (18:30) is the closing shift.
There are eight “Collegia Advisors” (CAs) who are employed to supervise and work at LIFE Collegium. One CA is designated as the “Senior CA” and has special scheduling considerations different from the other seven (“CA” will henceforth refer to the seven “regular” CAs and the “Senior CA” will explicitly be referred to as such).
Regular CAs
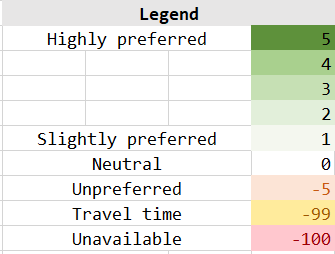
Each CA provides a timetable of their availability and preferences using the following numerical system:
Each provides a 22 x 5 table like so:
(Note: CAs are UBC students so blocks of unavailability are often classes.)
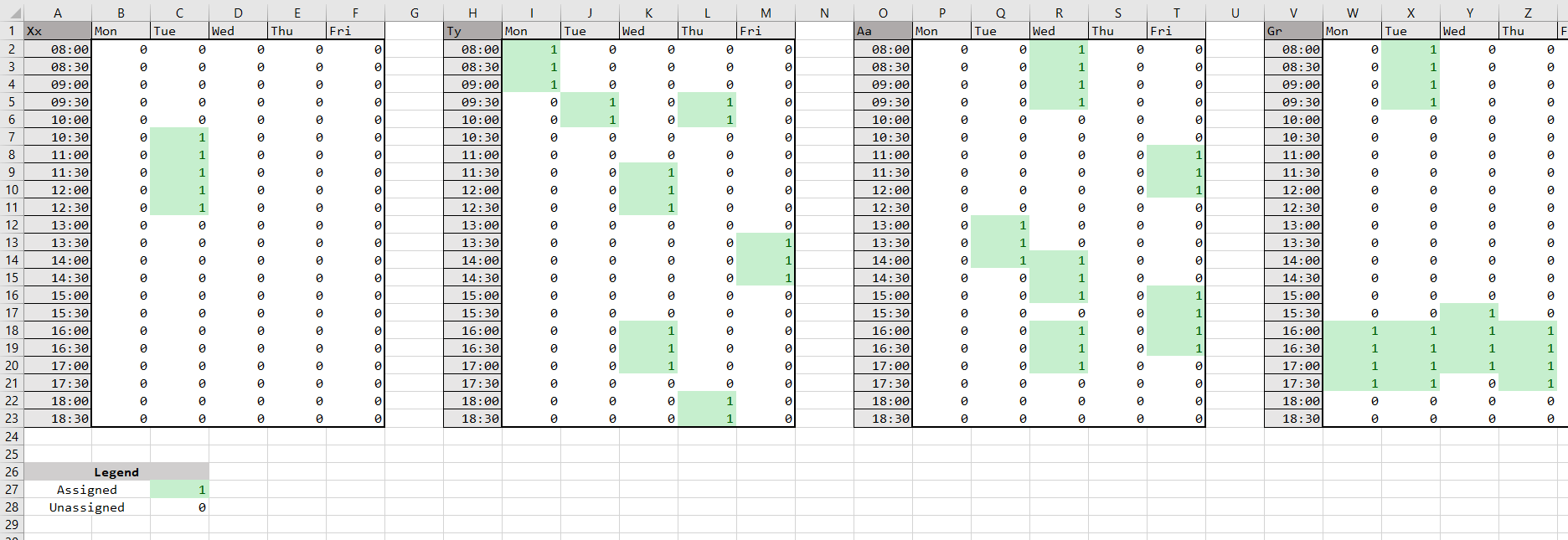
We collect all of the employee availability timetables into one Excel sheet.
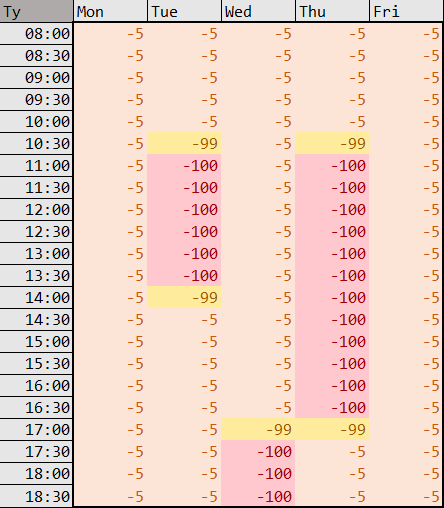
The Senior CA
Our scheduling methodology is to accommodate the seven CAs as best as possible and then schedule the Senior CA to pick up any leftover shifts. Hence, our output will only schedule the Senior CA when absolutely necessary. To do this, the Senior CA’s timetable will appear as such:
Excluding unavailable times, (-5) is the blanket availability score. Essentially, the Senior CA should only be assigned to slots that are highly negative (-99 or -100) for the other CAs and not when other CAs are available (with a score greater than or equal to 0).
The model does not force a minimum number of working hours for the Senior CA. The idea is that the Senior CA should assign themselves more slots as they see fit after seeing their “mandated” slots.
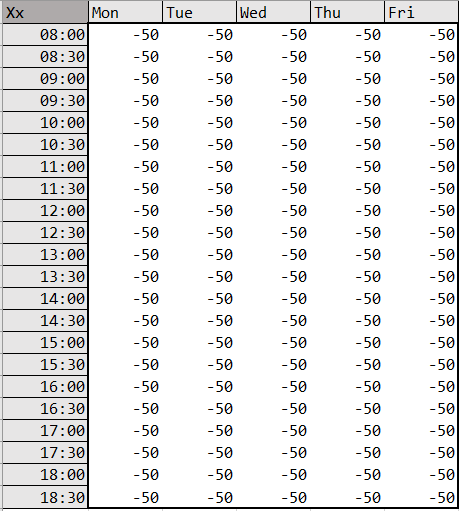
The Placeholder
It is possible that none of the CAs or the Senior CA can work a certain time slot (which occurred in 2018-19 Term 2). In this case, a “substitute” or “placeholder CA” is required. This placeholder (called “Xx”) has the following timetable:
The blanket (-50) availability score ensures that they are only assigned when all other staff members have scores of (-100) or (-99). The final output will show which hours, if any, a substitute must be hired.
Reading into Julia with Taro
In our Excel sheet, Xx is always the first timetable, followed by the Senior CA, then the rest of the CAs in arbitrary order.
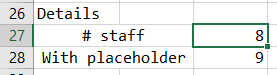
The number of employees must be manually entered into cell C27 so as to tell the program how far to read into the sheet. C28, which automatically includes the placeholder, is ultimately read by the program and becomes staff.
Now, we use the Taro package to read the tables in Excel into Julia arrays. We take advantage of the even spacing of the 22 x 5 tables to obtain the amount specified in C28.
# get staff availability tables
# top left cell on row 2, bot right cell on row 23
# each table separated by 7 cells
staff_array = [] # with preference/availability data
staff_dict = Dict{Integer, String}() # with names of staff
for i in 0:staff - 1
range = string(numtocol(7 * i + 2),
"2:",
numtocol(7 * i + 6),
"23")
push!(staff_array,
DataFrame(Taro.readxl("availability.xlsx", "availability",
range, header = false)))
staff_dict[i + 1] = String(getCellValue(getCell(getRow(getSheet(
Workbook("availability.xlsx"), "availability"), 0), 7 * i)))
end
Each employee is now enumerated with a value k (1 to 9). Importantly, k = 1 represents the placeholder and k = 2 represents the Senior CA.
Unlike the 2-dimensional availability array in the SPL scheduling project, this availability array is 3-dimensional (22 slots/day x 5 days x 9 employees):
# create 3D availability array
av_matrix = Array{Int8}(undef, 22, 5, staff)
for k in 1:staff
for i in 1:22
for j in 1:5
av_matrix[i,j,k] = Matrix(staff_array[k])[i,j]
end
end
end
Model
We use Gurobi for our model since it supports the quadratic objective function.
Variable
Our binary assignment variable is defined as follows:
# 22 x 5 x staff binary assignment 3d matrix
# 1 if employee k assigned to shift (i,j), 0 otherwise
@variable(m, x[1:22, 1:5, 1:staff], Bin)
Objective Function
Our objective function, similar to the SPL objective function, will be the sum of the availability scores of assigned shifts to represent how “preferred” a schedule is. By maximizing this score, in theory more people get shifts they want.
However, with our objective function, we also have to reward continuous shifts in order to avoid “swiss-cheese” schedules like
Assignment of any given shift provides opportunity for the adjacent shifts (the half-hour shift before and after) to receive a bonus. This bonus will be a multiplier (of some positive value). For example, if Mon 11:00 is assigned, then assigning 10:30 or 11:30 can multiply the availability score of those shifts by the bonus, making continuous shifts highly rewarding. Here, we choose the bonus to be 10 (arbitrarily chosen with respect to the availability scores).
# objective: rewards continuous shifts
# special cases k = 1 (placeholder)
# k = 2 (Senior CA)
@objective(m, Max,
sum(av_matrix[i, j, k] * x[i, j, k] +
x[i, j, k] * (10 * av_matrix[i + 1, j, k] * x[i + 1, j, k]
+ 10 * av_matrix[i - 1, j, k] * x[i - 1, j, k])
for i in 2:21, j in 1:5, k in 3:staff)
# special cases k = 1,2
+ sum(av_matrix[i, j, k] * x[i, j, k] for i in 1:22, j in 1:5, k in 1:2))
Note that the placeholder and Senior CA are exempt from this continuous reward.
Ideally, this will promote shift clustering so as to use the bonus as much as possible. We see how the number of bonus multipliers grows:
| Continuous shifts | Occurrences of bonus multiplier |
|---|---|
| 1 | 0 |
| 2 | 2 |
| 3 | 4 |
| n | 2(n - 1) |
In the future, we may experiment with different bonus multipliers and bonus multipliers that reach across two or more shifts. As well, we may investigate other methods of promoting or enforcing continuous shifts.
Note that we do not want to an outright ban of assignment structures such as
We see that this employee’s corresponding availability looks like
Hence, this CA has an obligation for a half-hour, yet would like to work before and after this unavailability. Our continuous shift reward ensures that this type of assignment is not impossible, and only used when necessary.
Constraints
Refer to GitHub for the complete code. We explicitly explore some of the constraints here.
Total time constraints
- Each CA works exactly 10 hours in a week.
- The Senior CA works maximum 13 hours in a week.
- The Senior CA works maximum 2 opening/closing shifts in a week.
- This is not a hard constraint provided by LIFE Collegium. Generally, CAs do not like opening/closing (as I’ve been told first-hand during my time at LIFE). Hence, most people would assign opening/closing shifts (0) or (-5). The resulting output would tend to assign them other shifts which maximized the availability scores. In the end, the Senior CA was left picking up the many opening/closing shifts. The hard limit of 2 is to avoid this. Another way to do this is guarantee each CA works a certain amount of opening/closing shifts.
Number of workers constraints
- There are 1 - 2 people working at any given time.
- Exceptions: opening/closing, weekly meeting.
- There is exactly 1 person per opening/closing shift.
- All CAs attend the weekly 90 minute meeting.
- For 2018-19 Term 2, this was Wed 16:00 - 17:30.
Shift length constraints
- Each shift is at least 1 hour long.
- Each shift is at most 4 hours long.
The translation of the minimum shift length constraint into code is the most interesting of the bunch. We want to translate the following conditional: “If timeslot i is assigned in day j for employee k, then either i - 1 or i + 1 is also assigned for that day and employee.” Of course, we need to account for edge cases in which i - 1 is 0 or i + 1 is 23.
Initially, I tried to implement this constraint with ConditionalJuMP. However the consequent of the conditional being a disjunction proved somewhat troublesome. Later, I found a much more elegant representation of the constraint:
# cons3: each shift is at least 1hr
for i in 2:21
for j in 1:5
for k in 1:staff
@constraint(m, x[i - 1, j, k] + x[i + 1, j, k] >= x[i, j, k])
end
end
end
In essence, the sum of the two adjacent shifts must be greater than the shift itself. It works out for all of the assignment cases for three adjacent shifts that this is equivalent to the conditional described above. Whether or not this type of translation of conditional and disjunction into a sum and inequality can scale up to say, 90 minute shifts and so on is an interesting point of further exploration. For now, this manages the job just fine, if only by sheer chance.
As of yet, the 4 hour maximum constraint has been unnecessary so it is not included. For completeness, this will be added in the future.
Result
After running the solver, we can collect the assignments to each timeslot and see how much overlap there is:
Solution count 5: 5625 5601 5570 ... 1052
Optimal solution found (tolerance 1.00e-04)
Best objective 5.625000000000e+03, best bound 5.625000000000e+03, gap 0.0000%
Objective value: 5625.0
22×5 Array{Array{Int64,1},2}:
[2] [4] [3] [6] [8]
[2] [4] [3] [6] [8]
[2] [4] [3] [6] [8]
[8] [2, 4] [3] [2] [8]
[6, 8] [2] [6] [2] [6]
[6, 8] [1] [6] [8] [6]
[6, 8] [1] [6] [8] [3, 6]
[9] [1] [2] [8] [3, 9]
[7, 9] [1] [2] [8] [3, 9]
[7, 9] [1] [2] [8] [9]
[7, 9] [3] [7] [5, 8] [9]
[5, 7] [3] [7] [5] [2]
[5] [3] [3, 7] [5] [2]
[5, 7] [5, 7] [3] [5, 7] [2]
[5, 7] [5, 7] [3] [7] [3]
[5, 7] [5, 7] [4, 9] [7] [3]
[4, 7] [4, 5] [2, 3, 4, 5, 6, 7, 8, 9] [4, 9] [3]
[4, 9] [4, 5] [2, 3, 4, 5, 6, 7, 8, 9] [4, 9] [3, 6]
[4, 9] [4] [2, 3, 4, 5, 6, 7, 8, 9] [4, 9] [6]
[4, 9] [4] [8] [4] [5, 6]
[9] [6] [8] [2] [5]
[9] [6] [8] [2] [5]
Like with our SPL schedule, we can also use Taro to write the result to Excel (in another workbook as a safeguard against corrupting the availability file). Reading this result from our original Excel file gives a more human-friendly view of the result:
We see that in the end, no one was available for certain shifts on Tuesday, so a substitute is required. In general, the schedules look good with minimal swiss-cheesing, so our objective function did its job nicely!
Extensions and Improvements
- Find a way to scale the minimum shift length constraint.
- Add the maximum shift length constraint.
- Have a way to visualize the overlapping shifts nicely.
- Have the weekly meeting time be entered on the main sheet and change in the constraint accordingly.
- Investigate different relative weights of preferences and different bonuses for the continuous reward.
- Investigate different ways to encourage continuous shifts.
- Explore ways to reward different people working opening/closing shifts.
- Output the other possible (sub-)optimal solutions.